Matematika: Između brojeva i stvarnosti

Pomislite samo na Neptun. Zašto? Zato što je, na prvi pogled, nevidljiv.

Čak i uz pomoć dobrog teleskopa.

Na 4.3 milijarde kilometara od Zemlje, osma planeta našeg Sunčevog sistema izgleda kao bela tačkica na nebu.

• Kako žive levoruki u svetu desnorukih
• Zbog čega je broj 6174 misteriozan za matematičare

Zbog toga su nas planete koje su bliže Zemlji, kao što su Venera ili Mars - a koje toliko jarko blešte na noćnom nebu - od davnina oduševljavale.

Za razliku od njih, za postojanje Neptuna saznalo se tek u 19. veku.

Otkriće ove planete bilo je važno iz dva razloga.

Uran i Neptun

Ne samo da smo pronašli novog suseda, već je „Neptun obeležio početak našeg istraživanja Sunčevog sistema, zato što nije otkriven gledanjem u nebo našim očima ili uz pomoć teleskopa", kaže Lusi Grin, astrofizičarka iz Malardove svemirske naučne laboratorije sa Univerzitetskog koledža u Londonu.

Neptun je otkriven zahvaljujući matematici.

U devetnaestom veku, pravilno su shvaćeni Njutnovi zakoni gravitacije, a sa njima su mogle da se predvide i orbite planeta koje se obrću oko Sunca.

Sem orbite Urana - otkriveno je da ona blago odstupa od očekivane putanje.

U ono vreme, to je bila najdalja poznata planeta od Sunca i neki naučnici su spekulisali da možda Njutnovi zakoni gravitacije ne funkcionišu na tolikoj udaljenosti.

Ali drugi su se pouzdali u matematiku i shvatili da u blizini Urana mora da postoji nekakvo ogromno telo koje menja putanju ove planete oko Sunca.

„Oni su izračunali šta, kako i gde. I kad su usmerili teleskop u pravcu oblasti na koju je ukazala matematika, otkrivena je nova planeta", kaže Grin.

Otkriće Neptuna zabeleženo je u istoriji kao dokaz da matematika nije izmišljena, već da postoji.

I upravo je to zaintrigiralo slušaoca BBC emisije Kraud Sajens Serđa Huarkajua iz Perua.

„Od Galileja koji je mogao da predvidi brzinu lopte dok se kotrlja niz padinu, do, na primer, postojanja Higsovog bozona, predviđenog matematikom pre nego što je čestica pronađena u stvarnosti, ta moć da se predvidi postojanje stvari koje nisu viđene golim okom deluje mi fantastično", napisao je on.

„Da li je matematika model, opis, metafora za stvarnost... ili je ona stvarnost sama?"

Ovo pitanje hiljadama godina muči i filozofe - i dalje je uzrok velikog neslaganja.

Ne postoji negativna torta

Gotovo je sigurno da su ljudi počeli da se bave matematikom iz ovozemaljskih razloga, kao što je prebrojavanje i merenje stvari, tako da počnimo odatle.

Uzmimo kao primer tortu.

Matematika može da nam saopšti svakakve stvari o toj torti: njene dimenzije, težinu, kako je rasparčati - i sve to na vrlo opipljiv način.

A torta može da nam pokaže da matematika dopire tamo gde stvarnost ne doseže.

Ukoliko pojedete trećinu torte, ostale su vam dve trećine.

Za sada je sve kako treba. Ako pojedete i preostalu trećinu, pa još jednu, ne ostaje vam ništa.

„Mi opisujemo mentalne konture naših predaka", kaže Aleks Belos, autor matematičkih knjiga.

„Oni su koristili praktičnu matematiku da bi merili i brojali, ali nisu stigli do negativnih brojeva."

Ako se vaš koncept stvarnosti sastoji od predmeta koje možete da izmerite i prebrojite, teško vam je da zamislite bilo šta što je manje od nule.

O dugovima i negativnim brojevima

Čim pojedete i poslednje mrvice te torte, gotovo je: ne postoji negativna torta.

Međutim, kaže Belos, postoji oblast u kojoj koristite negativne brojeve i potpuno je prirodno da razmišljate o njima.

Belos govori o novcu.

„Možete da posedujete novac, ali isto tako možete i da ga dugujete. Prva praktična upotreba negativnih brojeva bila je u kontekstu bankovnih računa i dugovanja", kaže on.

Ukoliko dugujete pet dolara, a ja vam dam tu sumu, imaćete nula dolara.

• Istine i zablude o neuronauci
• Preispitivanja Čarlsa Darvina oko „gnusne misterije“ koja ga je mučila do kraja života

Na taj način stvarnost počinje sa negativnim brojevima.

Danas je teško razmišljati o matematici bez njih i to ne samo kada se radi o dugovanjima.

Za sada smo i dalje duboko ukorenjeni u stvarnosti.

Ali kad krenete da se igrate sa negativnim brojevima, počinju da se dešavaju neke vrlo neobične stvari.

Ogromna enigma

Ako pomnožite dva takva broja, rezultat je pozitivan broj.

Dakle -1 x -1 = 1 i tako stižemo do istinske enigme.

„Ako počnete da se igrate s jednačinama koje sadrže i negativne i pozitivne brojeve, stići ćete do:

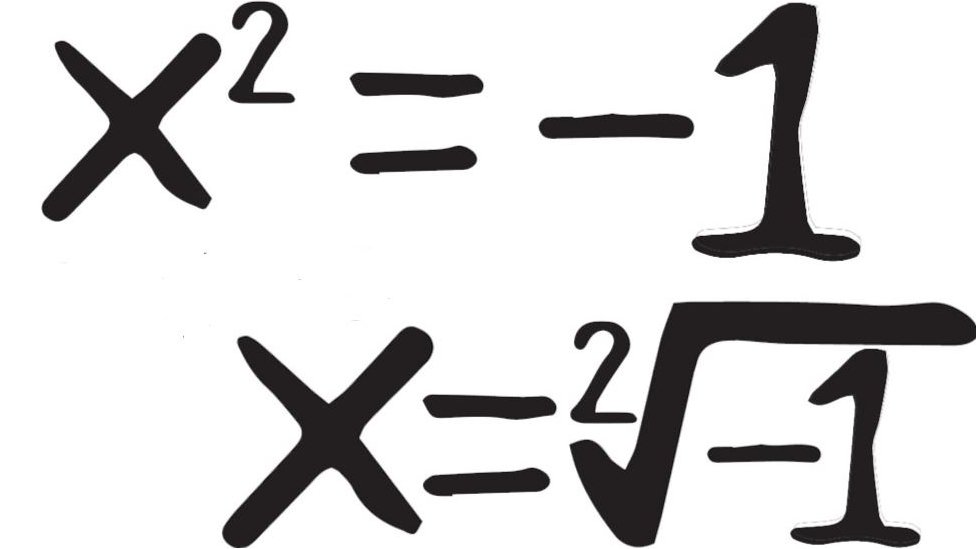
„Šta li je to? Kako kad kvadrirate nešto stižete do rezultata -1!", kaže Belos.

„To ne može da bude pozitivan broj jer kad ga kvadrirate - iliti pomnožite sa samim sobom - rezultat je pozitivan broj; a ne može da bude ni negativan broj, iz istog tog razloga", kaže on.

„Kad se to desilo prvi put, ljudi su mislili da se radi o apsurdu."

„Ali, malo po malo, matematičari su počeli da govore: 'Jeste, apsurdno je, ali kad to koristim u radu, dobijam pravi odgovor. Prepustimo filozofima da prokljuve šta bi to moglo da bude. Nama matematičarima potrebni su odgovori i, ukoliko nam to pomogne da ih nađemo, onda je to u redu."

I upravo smo sada napustili stvarnost.

Ali, u svakom slučaju, matematika i dalje služe objašnjava vrlo stvaran svet u kom živimo.

Imaginarno

„Kvadratni koren iz -1 zove se 'imaginarni broj', što je užasno ime zato što stičete utisak da je matematika do tog trenutka bila realna, a onda je odjednom postala imaginarna", kaže Belos.

„Ne, matematika je od samog početka imaginarna. Možemo da govorimo o tri torte, ali mi vidimo samo torte, ne vidimo 'tri': tri je apstrakcija", ističe on.

„Isto vam je kad imate imaginarne brojeve. Deluje potpuno ludo, ali čim počnete da razumete kako se oni uklapaju, sve postaje logično. I ponašanje onoga što zovemo realnim brojevima sa imaginarnim brojevima - sve do nečega što zovemo složenim brojevima, briljantan je rečnik da se opišu stvari kao što je rotacija."

„Ovih dana, kvadratni koren od -1 realan je koliko i sam -1", čak i ako nam je teško da razumemo -1, baš kao što je to bilo našim precima.

Samo bez panike

Ako ste se malo pogubili, ništa ne brinite - samo nastavite da čitate i sve će vam biti jasno. Zaista.

Složeni brojevi omogućavaju rešenja nekih jednačina koje nemaju rešenja u realnim brojevima.

Oni su neverovatno praktični za razumevanje stvarnosti i služe kao alatke za gotovo sve što uključuje rotaciju ili talase.

Koriste se u elektrotehnici, radarima, medicinskim snimanjima i mogu da se primene na razumevanje subatomskih čestica.

Ali kako to da nešto što izgleda kao da postoji samo u matematičkim snovima na kraju ispadne toliko korisno u stvarnom svetu?

Za neke, kao što je mađarski fizičar iz dvadesetog veka Judžin Vigner, to predstavlja skoro pa čudo.

Vigner se pozvao na složene brojeve u uticajnom eseju iz 1960. godine, Nerazumna efikasnost matematike u prirodnim naukama.

Nerazumna efikasnost

Ali ako su ljudi osmislili matematiku upravo da bi opisali stvarnost, zar nije onda logično što ona to i radi? Šta je nerazumno u vezi s tim?

Obratimo se sada nekome ko se neprestano kreće između filozofije i matematike: ekspertu za filozofiju fizike Elenor Noks.

„Ukoliko smo izumeli matematiku da bi nam pomogla da razumemo fizičke sisteme, istina je da je veoma logično da ona to i radi. Ali čini se da se matematika ispočetka nije razvijala na taj način", objašnjava ona.

„Ima mnogo slučajeva u kojima su matematičari uradili nešto samo zato što su bili zainteresovani za to, a u nekom kasnijem periodu ispostavilo se da je upravo to bilo neophodno za neko ključno otkriće u fizici.

„Slavan primer je neeuklidska geometrija", kaže Noks, govoreći o grani geometrije kojom su se bavili mnogi matematičari krajem 19. veka - pre svega zato što su mislili da je interesantna.

„Mislili su da čitav naš svet može da se opiše preko euklidske geometrije, one koju učite u školi. Pravila pravog ugla, da uglovi trougla u zbiru daju 180 stepeni, na primer."

Matematičari devetnaestog veka nisu se bacili na obaranje euklidske geometrije. Prosto su samo istraživali i pronašli neke zanimljive matematičke strukture.

„U dvadesetom veku, kad je Albertu Ajnštajnu bila potrebna teorija kojom bi opisao pravila prostora i vremena za opštu teoriju relativnosti, upravo mu je pomogla neeuklidska geometrija - on prosto ne bi uspeo da nije bilo nje", dodaje Noks.

„Danas mi mislimo da svet ima strukturu te geometrije koja je nekada bila krajnje neobična, a nijedan matematičar koji je krenuo da radi na njoj nije predvideo to konkretno otkriće", zaključuje ona.

Takvi slučajevi nas navode na razmišljanje da, ukoliko nije baš čudnovat, odnos matematike prema stvarnosti makar je poprilično zapanjujuć.

Fundamentalna stvarnost

Imajući u vidu pravac u kom se razvija moderna fizika, nama običnim smrtnicima teško je da razumemo komplikovanu matematiku i neobičnu stvarnost koju ona opisuje.

Ali to možda i ne iznenađuje: ne postoji razlog zašto bi svakodnevna stvarnost koju doživljavamo putem naših čula bila fundamentalna stvarnost univerzuma.

Ono što iznenađuje je da se čini da matematika ume da istraži mnogo više nego što nam naša čula dopuštaju.

Međutim, u potrazi za fundamentalnom stvarnošću, hoće li se desiti da matematika dosegne maksimum sposobnosti da je opiše?

„Dvadeseti vek nam je podario dve od naših najuspešnijih fizičkih teorija: kvantnu mehaniku (svet na nivou ultra-malog, atoma i subatoma) i teoriju opšte relativnosti", kaže Noks.

„Ispostavlja se da je postizanje toga da matematika objedini te dve teorije izuzetno komplikovano."

„Nemamo koherentan okvir za razumevanje toga kako te dve teorije mogu da funkcionišu u istom svetu - kako one mogu da opišu istu stvarnost", dodaje ona.

„Morate da se izborite sa zapanjujućim nivoima složenosti a da ne uspete, za sada, da spojite ono što ste promislili sa eksperimentima."

Međutim, kao što smo već videli ranije, mnogo toga je započelo upravo tako: kao ideja u potrazi za praktičnom funkcijom.

Ali da li smo sada možda udarili u zid?

• Otkriveni novi Ajnštajnovi rukopisi
• Hirurzi i dalje koriste nacističku knjigu anatomije

„U ovom trenutku, čovek bi lako mogao da zaključi da smo do sada imali veoma, veoma mnogo sreće što je matematika uspevala da opiše naš univerzum", kaže Noks.

„Druga opcija je da pomislite kako matematika opisuje samo delove sveta, ali ne i njega u celosti."

„Ili možda da je razumevanje sveta u njegovoj celosti veoma komplikovano."

„Ili da je matematika vraški komplikovana, da je previše za nas ili da je još nismo razumeli, ali da jednog dana hoćemo", kaže ona.

Velika razlika

Možda i ne bi trebalo da nas iznenadi što je ponekad đavolski teško uskladiti matematičke zakone sa zakonima fizičke stvarnosti. Na kraju krajeva, oni nisu isto.

Kao što je Ajnštajn jednom rekao: „Što se više odnose na stvarnost, matematički zakoni više postaju nesigurni; a što su sigurniji, manje se odnose na stvarnost."

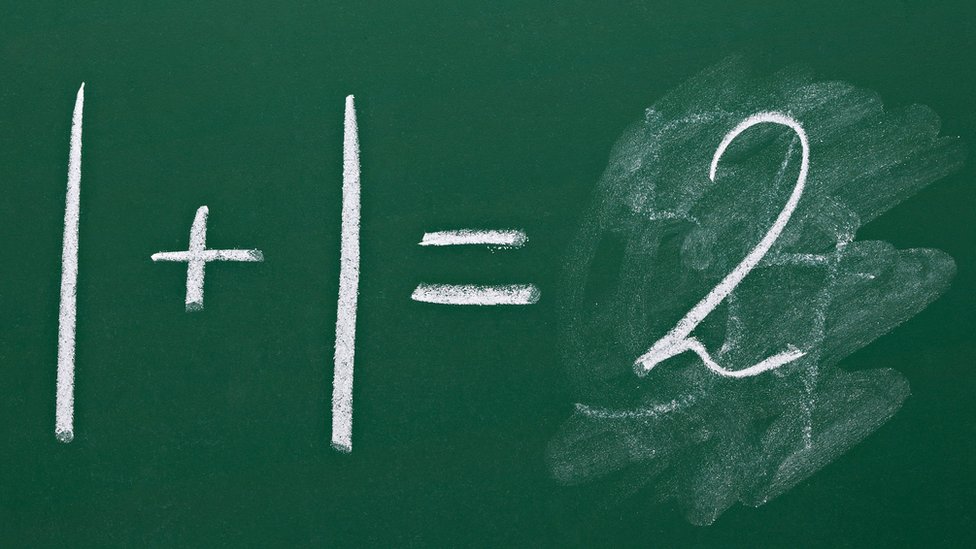
Noks objašnjava: „Matematika ima jednu posebnu karakteristiku: apsolutno je istinita ili neistinita. Ako dokažem nešto u matematici, niko ne može da opovrgne tu činjenicu."

„Fizički zakoni nisu takvi. To je jedna od velikih razlika među njima."

„Često smo grešili u zakonima. Njutnovi zakoni su predivni, elegantni i u nekim slučajevima validni, ali oni nisu kompletna istina. Nema sumnje da će se u budućnosti pokazati da su Ajnštajnovi zakoni takođe aproksimativni", predvidela je ova filozofkinja fizike.

Otkrivena ili izmišljena?

Odakle dolazi matematika?

To je pitanje za matematičara.

Judžinija Čeng je gostujuća naučnica Škole umetničkog instituta u Čikagu.

Ona može da odgovori na pitanje da li je matematika nešto što je otkriveno ili izmišljeno.

„Zaista mislim da ja otkrivam koncepte a izmišljam načine razmišljanja o njima. Kada radim apstraktno istraživanje, osećam se kao da lutam kroz apstraktnu džunglu u potrazi za stvarima i onda izmišljam način na koji ću da govorim i teoretišem o njima kako bih mogla da organizujem vlastite misli i prenesem ih drugima", kaže ona.

Čeng radi na polju Teorije kategorija (ponekad zvane „matematikom matematike"), koja pokušava da premosti jaz između različitih oblasti u matematici.

„Šta je uopšte stvarno?"

Teško je zamisliti nešto apstraktnije od toga, tako da smo je pitali da li misli da se matematika koju ona proučava odnosi i na stvarnost.

„Kad me ljudi pitaju za stvarnost, ja želim da odgovorim sa: a šta je uopšte stvarno?"

„Ono što mi zovemo 'stvarnošću' zapravo su halucinacije koje doživljavamo kao stvarne zato što smo svi skloni da ih percipiramo na isti način."

„Ljudi kažu da brojevi nisu stvarni zato što ne možete da ih dodirnete. Ali ima mnogo stvari koje su stvarne ali ne mogu da ih dodirnem, kao što je, na primer, glad", objašnjava ona.

„Zato više volim da govorim o konkretnim stvarima - onima koje možemo da dodirnemo i sa kojima možemo da imamo direktnu interakciju - i o apstraktnim stvarima - sa kojima imamo interakciju u našem mozgu."

„Matematika je apstraktna, ali apstraktna ideja može da bude onoliko stvarna kao i bilo šta drugo."

Šta je stvarno?

S jedne strane, neko može da tvrdi da je matematika stvarnost.

Pomislite samo, na primer, na našu biologiju, koja se sastoji od hemije, a kojom suštinski vladaju fizički zakoni... i mi tako stižemo do brojeva.

Ili pomislite na plavo nebo, koje se objašnjava talasnim dužinama prelamanja svetlosti... i sve su to brojevi.

Čini se da je, ako zakopate dovoljno duboko, fizička stvarnost suštinski matematička.

Čini se da matematika, međutim, ne može da nam kaže ništa značajno o nekim od najvažnijih životnih pitanja, kao što su ljubav, glad ili smrtnost.

I tako, od svih stvarno velikih pitanja, sa sigurnošću možemo da odgovorimo na samo jedno: možda nećemo uspeti da nađemo konačne odgovore na pitanje koje je postavio Serđo Huarkaja iz Perua.

Zapravo, sada sa sigurnošću možemo da kažemo da nećemo.

Ali ih je zato vredelo tražiti.

Pratite nas na Fejsbuku i Tweets by bbcnasrpskom Ako imate predlog teme za nas, javite se na [email protected]